| / Home |
| S-Archive | Download Fortran - Download Script |
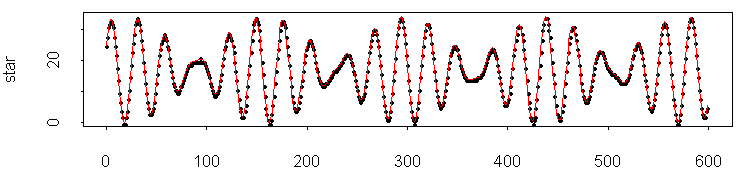
| pronyfreq | Frequency Estimation |
| y | numeric vector. |
| nfreq | number of frequencies to estimate. | |
| constant | logical variable, indicating whether to include a constant in the model. | |
| tol | tolerance indicating required accuracy. | |
| maxit | maximum number of iterations. | |
| trace | logical variable. If true then the top half of the Prony vector and the smallest and largest eigenvalues of the Prony matrix are output at each iteration. | |
| warnings | logical variable. If false, then run quietly without issuing warnings about non-convergence. Useful when using pronyfreq for a few iterations to get starting values for another estimation technique. |
| prony | numeric vector of coefficients of the Prony difference equation. | |
| freq | numeric vector of frequencies. | |
| coef | numeric vector of coefficients. The first component is the constant term, then the coefficients of cos(f*t) for each frequency, then the coefficients of sin(f*t) for each frequency. | |
| fitted | numeric vector. The value of the sum of sinusoidal frequencies. | |
| residuals | numeric vector, equal to y - fitted |
| S-Archive | Download Fortran - Download Script |
Gordon Smyth. Copyright © 1996-2016. Last modified: 10 February 2004